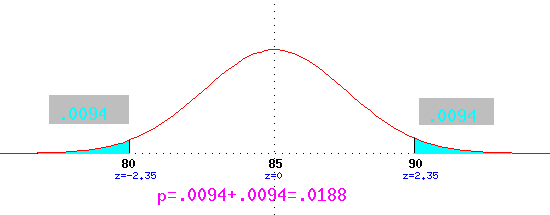
A test of hypotheis entails:

Competencies: If the standard deviation is known to be equal to 12, and your null hypothesis is that the mean of the population is equal to 15, at what level (p-value) is x-bar = 13.5 based on a sample of size 200 significant? Would you reject the null hypothesis at the 10% significance level? 5% significance level? 1% significance level?
Reflection: What is the relationship between a two tailed test of hypothesis and a confidence interval?