Normal distribution (mu,sigma)
The ubiquitousness of the normal distribution is clearly not with mean 0 and
standard deviation one; for example, many data such as heights and weights are
never negative. But if data is normally distributed, it can be transformed
to have mean 0 and standard deviation 1, and the transformed data will be
standard normal for which the tables can be used. In particular, if some
data {x} are normally distributed, the corresponding {z} will be normal with
mean 0 and standard deviation 1 where the correspondence between the {x} and
{z} is given by z = (x-mu)/sigma. Such z's are called z-scores. By
subtracting mu, the mean has been shifted to 0, by dividing by sigma the
standard deviation has been changed to 1.
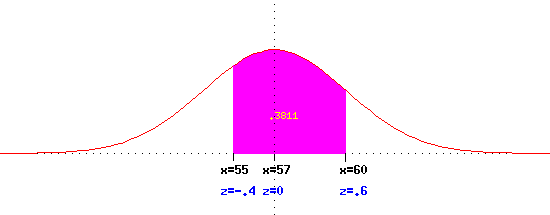
Assume that height is normally distributed with mean=57 and standard deviation
= 5. What fraction of people are between the heights of 55 and 60 inches?
The z-scores corresponding to 55 and 60 are (55-57)/5 = -.4 and
(60-57)/5 = .6. At this stage the calculations
are those for the standard normal distribution. From the table we get
-.4 corresponds to .3446, .6 corresponds to .7257, hence the area between is
.7257-.3446=.3811. The following figure may clarify what we have done.
If height has a mean of 67 and a standard deviation of 5, we can also ask what
height 20% of the students will be shorter than. The first step is to
convert the area (relative frequency) to a
z-value using the table. Since we have specified the area to the left, we
look for .2 in the body of the table, and find .2005 which corresponds to the
z-value -.84.

Then we must rearrange the formula z = (x-mu)/sigma to x = mu + (z)(sigma)
to get back to inches from standard deviation units. 67+(-.84)(5)=62.8.
(Drawing a picture may help you remember when to add or subtract.)
If data is normally distributed, but the mean is not 0 and/or the standard
deviation is not one, there are two stages to problems:
- If the interval is specified and you are looking for the relative
frequency (probability): first convert from x-values to z-scores, then use
the normal table to find the area (relative frequency, probability).
- If the relative frequency (probability) is specified, first use the normal
table to find the z-values, then convert the z-values to x-values.
Applets: A good applet for showing the correspondence between raw data
and z-scores by Gary McClelland is linked here
(you need to hit enter after entering your values). An alternative
version is also available.
Competencies:
If height is normally distributed with mean 69 inches and standard deviation 4
inches (N(69, 4²)), what fraction of the people are between 60 and 70
inches in height?
If height is normally distributed with mean 69 inches and standard deviation 4
inches (N(69, 4²)), what height are 10% of the people taller than?
return to index
Questions?

